⇒ A rotation through 90° anticlockwise about the origin maps the point (1, 0) to the point (0, 1) and the point (0, 1) to the point (-1, 0)

⇒ So the matrix representing this transformation is \( \begin{bmatrix}0 & -1 \\1 & 0 \end{bmatrix} \)

⇒ Reflection in the x-axis leaves the point (1, 0) unchanged but maps the point (0, 1) to the point (0, -1)

⇒ So the matrix representing this transformation is \( \begin{bmatrix}1 & 0 \\0 & -1 \end{bmatrix} \)

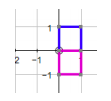
⇒ Having looked at those examples of reflection and rotation, we can see that any linear transformation can be defined by the effect it has on the unit vectors \( \left(\begin{array}{c}0\\ 1\end{array}\right) \) and \( \left(\begin{array}{c}1\\ 0\end{array}\right) \)

⇒ Thus the transformation represented by the matrix M = \( \begin{bmatrix}a & b \\c & d \end{bmatrix} \) will map \( \left(\begin{array}{c}1\\ 0\end{array}\right) \) to \( \left(\begin{array}{c}a\\ c\end{array}\right) \) and \( \left(\begin{array}{c}0\\ 1\end{array}\right) \) to \( \left(\begin{array}{c}b\\ d\end{array}\right) \)

⇒ Take a look at the following example to try and understand this further:

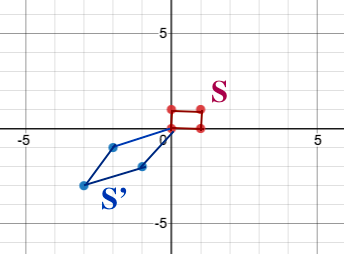
⇒ Here, the linear transformation \( \begin{bmatrix}-2 & -1 \\-1 & -2 \end{bmatrix} \) stretches and rotates the unit square S to produce the image S'

• Note that the origin does not change under a linear transformation (i.e. it remains at (0, 0))
• To find the fourth vertex of the new shape (-3, -3) you simply need to add the two image vectors together!
• Thus from our two initial unit vector - \( \left(\begin{array}{c}0\\ 1\end{array}\right) \) and \( \left(\begin{array}{c}1\\ 0\end{array}\right) \) - we can define the entire transformation

⇒ Points that do not move under the given transformation are called invariant points, and lines which do not move are called invariant lines

• The only invariant point in the above transformation is the origin, which is always an invariant point of any linear transformation

The transformation U, represented by the 2 x 2 matrix Q, is a reflection in the y-axis

a) Write down the matrix Q

b) Write down the equation of the invariant line of this transformation

⇒ So we want to consider the unit square and the effect that the transformation has on the unit vectors \( \left(\begin{array}{c}0\\ 1\end{array}\right) \) and \( \left(\begin{array}{c}1\\ 0\end{array}\right) \)

• This will completely define the transformation

⇒ Looking at part a, \( \left(\begin{array}{c}1 \\ 0\end{array}\right) \) maps to \( \left(\begin{array}{c}-1 \\ 0\end{array}\right) \) and \( \left(\begin{array}{c}0\\ 1\end{array}\right) \) maps to \( \left(\begin{array}{c}0\\ 1\end{array}\right) \)

• Hence matrix Q is \( \begin{bmatrix}-1 & 0 \\0 & 1 \end{bmatrix} \)

⇒ Looking at part b, we know then that the invariant line is the y-axis (as this stays the same after the transformation), so the equation of the invariant line is x = 0

• All of the points on the invariant line are invariant points

⇒ A reflection in the y-axis is represented by the matrix \( \begin{bmatrix}-1 & 0 \\0 & 1 \end{bmatrix} \) and has the y-axis (which has equation x = 0) as an invariant line

• This is exactly what we just saw in the above example

⇒ A reflection in the x-axis is represented by the matrix \( \begin{bmatrix}1 & 0 \\0 & -1 \end{bmatrix} \) and has the x-axis (which has equation y = 0) as an invariant line

P = \( \begin{bmatrix}0 & -1 \\-1 & 0 \end{bmatrix} \)

a) Describe fully the single geometrical transformation U represented by the matrix P

b) Given that U maps the point with coordinates (a,b) onto the point with coordinates (3 + 2a, b +1), find the values of a and b

⇒ We know that the transformation represented by the matrix M = \( \begin{bmatrix}a & b \\c & d \end{bmatrix} \) will map \( \left(\begin{array}{c}1\\ 0\end{array}\right) \) to \( \left(\begin{array}{c}a\\ c\end{array}\right) \) and \( \left(\begin{array}{c}0\\ 1\end{array}\right) \) to \( \left(\begin{array}{c}b\\ d\end{array}\right) \)

⇒ As a result, we know that \( \left(\begin{array}{c}1 \\ 0\end{array}\right) \) maps to \( \left(\begin{array}{c}0 \\ -1\end{array}\right) \) and \( \left(\begin{array}{c}0\\ 1\end{array}\right) \) maps to \( \left(\begin{array}{c}-1\\ 0\end{array}\right) \)

• Hence the transformation U represented by matrix P is a reflection in the line y = -x
• It may be easier to sketch this so you can visualise the transformation:

⇒ All question b is telling us is if we multiply matrix P by \( \left(\begin{array}{c}a\\ b\end{array}\right) \) we will get the coordinates \( \left(\begin{array}{c}3 + 2a\\ b + 1\end{array}\right) \)

• If you don't know how to multiply matrices, check out notes on multiplying matrices

⇒ Wecan then solve the resulting equations simultaneously to find the values of a and b

\( \begin{bmatrix}0 & -1 \\-1 & 0 \end{bmatrix}\left(\begin{array}{c}a\\ b\end{array}\right) = \left(\begin{array}{c}3 + 2a\\ b + 1\end{array}\right) \)

\( \left(\begin{array}{c}-b\\ -a\end{array}\right) = \left(\begin{array}{c}3 + 2a\\ b + 1\end{array}\right) \)

So -b = 3 + 2a (1)

and -a = b + 1 (2)

⇒ Solving simultaneous gives a = -2 and b = 1

⇒ A reflection in the line y = x (i.e. a diagnoal line sloping upwards through the origin) is represented by the matrix \( \begin{bmatrix}0 & 1 \\1 & 0 \end{bmatrix} \) and has invariant line with equation y = x

⇒ A reflection in the line y = -x (i.e. a diagnoal line sloping downwards through the origin) is represented by the matrix \( \begin{bmatrix}0 & -1 \\-1 & 0 \end{bmatrix} \) and has invariant line with equation y = -x

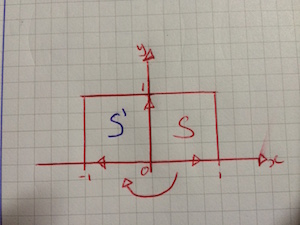
The transformation U, represented by the 2 x 2 matrix P, is a rotation of 180° about the point (0,0)

a) Write down the matrix P

b) Write down the coordinates of the invariant point of this transformation

⇒ The given rotation is shown in the following diagram:

⇒ Remember, if you need to find the matrix that represents a given transformation, it can help to draw a sketch transforming the unit square. Remember, the transformation is defined by its effect on the unit vectors

\( \left(\begin{array}{c}1 \\ 0\end{array}\right) \) maps to \( \left(\begin{array}{c}-1 \\ 0\end{array}\right) \) and \( \left(\begin{array}{c}0\\ 1\end{array}\right) \) maps to \( \left(\begin{array}{c}0\\ -1\end{array}\right) \)

• Hence the matrix is \( \begin{bmatrix}-1 & 0 \\0 & -1 \end{bmatrix} \)

⇒ For part b, the only point that does not move under this transformation is the origin, so the coordinates of the invariant point are (0, 0)

• As mentioned previously, the origin is invariant under any linear transformation

⇒ You need to be able to write down the matrix representing a rotation about any angle

⇒ The matrix representing a rotation through angle θ anticlockise about the origin is \( \begin{bmatrix}cosθ & -sinθ \\sinθ & cosθ \end{bmatrix} \)

⇒ The only invariant point is the origin (0, 0)

• If you are doing A-level further maths, this formula is given in the formulae booklet

⇒ You can read some more notes on this topic at Wolfram MathWorld

M = \( \Large\begin{bmatrix}-\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \end{bmatrix} \)

a) Describe geometrically the rotation represented by M

b) A square S has vertices at (1,0), (2,0), (2,1), and (1,1). Find the coordinates of the vertices of the image of S under the transformation described by M

Part A:

⇒ So we are told that M represents a rotation, therefore we want to compare the matrix (M) with \( \begin{bmatrix}cosθ & -sinθ \\sinθ & cosθ \end{bmatrix} \)

⇒ Using your calculator, you will notice that cos(135°) = \( -\frac{\sqrt{2}}{2} \) and sin(135°) = \( \frac{\sqrt{2}}{2} \)

⇒ Therefore, M is a rotation, anticlockwise, through 135° about (0, 0)

Part B:

⇒ To answer part B, we simply apply the matrix (M) to each vertex of S ((1,0), (2,0), (2,1), and (1,1)) in turn:

\( \Large\begin{bmatrix}-\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \end{bmatrix}\left(\begin{array}{c}1\\ 0\end{array}\right) = \left(\begin{array}{c}-\frac{\sqrt{2}}{2}\\ \frac{\sqrt{2}}{2}\end{array}\right) \)

\( \Large\begin{bmatrix}-\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \end{bmatrix}\left(\begin{array}{c}2\\ 0\end{array}\right) = \left(\begin{array}{c}-\sqrt{2}\\ \sqrt{2}\end{array}\right) \)

\( \Large\begin{bmatrix}-\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \end{bmatrix}\left(\begin{array}{c}2\\ 1\end{array}\right) = \left(\begin{array}{c}-\frac{3\sqrt{2}}{2}\\ \frac{\sqrt{2}}{2}\end{array}\right) \)

\( \Large\begin{bmatrix}-\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \end{bmatrix}\left(\begin{array}{c}1\\ 1\end{array}\right) = \left(\begin{array}{c}-\sqrt{2}\\ 0\end{array}\right) \)

⇒ Thus, the vertices of S' are \( (-\frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2}), (-\sqrt{2}, \sqrt{2}), (-\frac{3\sqrt{2}}{2}, \frac{\sqrt{2}}{2}), and (-\sqrt{2}, 0) \)

• Remember to give your answer like this, as coordinates, and not position vectors as it tells us in the question!!

⇒ Also see our notes on:

• Linear Transformations in Two Dimensions
• Enlargement and Stretches
• Successive Transformations
• Linear Transformations in Three Dimensions
• The Inverse of a Linear Transformation