⇒ It is possible to define a transformation in 2 dimensions by describing how a general point with a position vector \( \left(\begin{array}{c}x\\ y\end{array}\right) \) is transformed - the new point is called the image

The three transformations S, T, and U are defined as follows. Find the image of the point (2, 3) under each of these transformations

Example 1

S: \( \left(\begin{array}{c}x\\ y\end{array}\right) \mapsto \left(\begin{array}{c}x + 4\\ y - 1\end{array}\right) \)

• We need to substitute x = 2 and y = 3 into the expression

S: \( \left(\begin{array}{c}2\\ 3\end{array}\right) \mapsto \left(\begin{array}{c}2 + 4\\ 3 - 1\end{array}\right) = \left(\begin{array}{c}6\\ 2\end{array}\right) \)

• So the image is (6, 2)

Example 2

T: \( \left(\begin{array}{c}x\\ y\end{array}\right) \mapsto \left(\begin{array}{c}2x - y\\ x + y\end{array}\right) \)

• We want to substitute x = 2 and y = 3 into the equation

T: \( \left(\begin{array}{c}2\\ 3\end{array}\right) \mapsto \left(\begin{array}{c}2 \times 2 - 3\\ 2 + 3\end{array}\right) = \left(\begin{array}{c}1\\ 5\end{array}\right) \)

• So the image is (1, 5)

Example 3

U: \( \left(\begin{array}{c}x\\ y\end{array}\right) \mapsto \left(\begin{array}{c}2y\\ -x^{2}\end{array}\right) \)

• When x = 2, -x² = -2² = -4

U: \( \left(\begin{array}{c}2\\ 3\end{array}\right) \mapsto \left(\begin{array}{c}2 \times 3\\ -2^{2}\end{array}\right) = \left(\begin{array}{c}6\\ -4\end{array}\right) \)

• So the image is (6, -4)

⇒ With linear transformations, the transformations only involve linear terms in x and y

• In other words, T is a linear transformation (as you can write 2x - y and x + y in the forms ax + by). However, S represents a translation, but not a linear transformation since you cannot write x + 4 in the form ax + by

⇒ Any linear transformation sends the origin to the origin

• So, if we plugged in (0, 0) into a linear transformation we are going to get (0, 0) back out again i.e. it is mapped to itself

⇒ We can also represent any linear transfromation by a matrix:

• So the linear transformation T: \( \left(\begin{array}{c}x\\ y\end{array}\right) \mapsto \left(\begin{array}{c}ax + by\\ cx + dy\end{array}\right) \) can be represented by the matrix M = \( \begin{bmatrix}a & b \\c & d \end{bmatrix} \) since \( \begin{bmatrix}a & b \\c & d \end{bmatrix} \left(\begin{array}{c}x\\ y\end{array}\right)\) = \( \left(\begin{array}{c}ax + by\\ cx + dy\end{array}\right) \)
• If you haven't done so already, check out our notes on matrices, if you want to learn more about them. In particular, check out the notes on matrix multiplication if you are unsure about how this linear transformation can be represented by the matrix

⇒ For those of you who are looking for more of a challenge, why not check out the following notes from AMSI: Linear Transformation and Matrices

Find a matrix that represents the following linear transformation

Question 1

T: \( \left(\begin{array}{c}x\\ y\end{array}\right) \mapsto \left(\begin{array}{c}2y + x\\ 3x\end{array}\right) \)

⇒ This transformation is equivalent to T: \( \left(\begin{array}{c}x\\ y\end{array}\right) \mapsto \left(\begin{array}{c}1x + 2y\\ 3x + 0y\end{array}\right) \)

• So we have first written the transformation in the form \( \left(\begin{array}{c}ax + by\\ cx + dy\end{array}\right) \)

⇒ We can then use the coefficients of x and y to form the matrix

• So the matrix is \( \begin{bmatrix}1 & 2 \\3 & 0 \end{bmatrix} \)

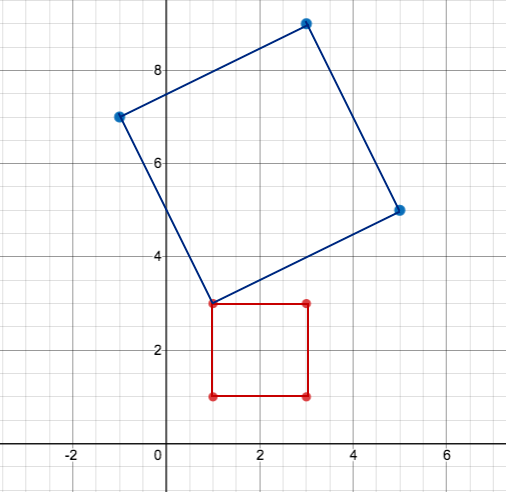
a) The square S has coordinates (1, 1), (3, 1), (3, 3) and (1, 3). Find the vertices of the imge of S uner the transformation given by the matrix M = \( \begin{bmatrix}-1 & 2 \\2 & 1 \end{bmatrix} \)

b) Sketch S and the image of S on a coordinate grid

⇒ To answer part a, we want to write each point as a column vector and then use the usual rule for multiplying matrices:

\( \begin{bmatrix}-1 & 2 \\2 & 1 \end{bmatrix} \left(\begin{array}{c}1\\ 1\end{array}\right)\) = \( \left(\begin{array}{c}1\\ 3\end{array}\right) \)

\( \begin{bmatrix}-1 & 2 \\2 & 1 \end{bmatrix} \left(\begin{array}{c}3\\ 1\end{array}\right)\) = \( \left(\begin{array}{c}-1\\ 7\end{array}\right) \)

\( \begin{bmatrix}-1 & 2 \\2 & 1 \end{bmatrix} \left(\begin{array}{c}3\\ 3\end{array}\right)\) = \( \left(\begin{array}{c}3\\ 9\end{array}\right) \)

\( \begin{bmatrix}-1 & 2 \\2 & 1 \end{bmatrix} \left(\begin{array}{c}1\\ 3\end{array}\right)\) = \( \left(\begin{array}{c}5\\ 9\end{array}\right) \)

⇒ Thus, the vertices of the image of S (i.e. S') lie at (1, 3), (-1, 7), (3, 9) and (5, 5)

⇒ To answer question b, we simply draw image S (which is a square with vertices (1, 1), (3, 1), (3, 3) and (1, 3)), and then draw S' on the same grapg (which is a square of vertices (1, 3), (-1, 7), (3, 9) and (5, 5))

⇒ Also see our notes on:

• Reflections and Rotations
• Enlargement and Stretches
• Successive Transformations
• Linear Transformations in Three Dimensions
• The Inverse of a Linear Transformation