⇒ Velocity-time graphs can be used to derive various different formulas

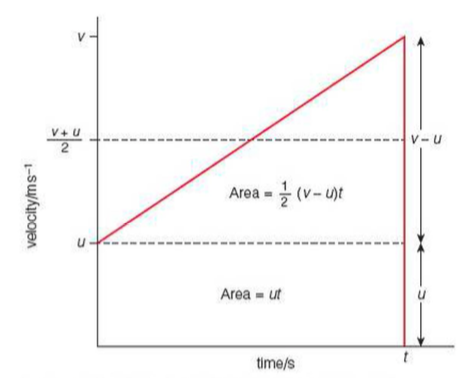
⇒ This velocity-time graph shows a vehicle increasing its velocity with a consent acceleration, a, from an initial velocity, u, to a final velocity, v, over a time, t

The first equation

The second equation

⇒ Displacement = average velocity x time

⇒ The average velocity is half way between the initial and final velocities

The third equation

⇒ The displacement can also be calculated from the area under the velocity-time graph

The fourth equation

⇒ This links velocity, acceleration and displacement...

⇒ There is no need to be able to derive these equations as they will be given in the exam. However, the derivation of the fourth equation is provided below:

Example 1

Example 2

Example 3

⇒ Galileo Galilei demonstrated that gravity accelerates all masses at the same rate, provided air resistance is very small

⇒ Knowing this, you could calculate the acceleration due to gravity using the following:

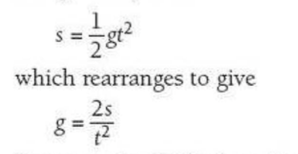
⇒ For example, you could imagine Galileo dropping a ball from the Leaning Tower of Pisa (55m high) and taking 3.25s to fall:

⇒ Terminal speed is the speed reached when the weight of an object in free fall is balanced by the drag forces (e.g. wind resistance) acting upwards

⇒ Drag is the name given to resistive forces experienced by an object moving through a fluid such as air or water

⇒ The size of the drag on a falling object increases with:

• Speed
• Surface area

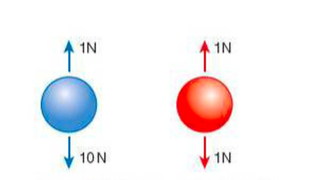
⇒ This image shows how drag affects two similar balls - they are the same size/shape, but the blue ball weighs 10N and the red ball weighs 1N

⇒ Both balls fall at the same speed and both have an upward drag of 1N, but the blue ball continues to accelerate as it has a resultant downward force whereas the red ball moves at a constant speed because the force of gravity is balanced by the drag

• In other words, the red ball has reached its terminal speed

⇒ Also see our notes on:

• Motion in a Straight Line
• Projectile Motion