⇒ You can generalise the rule for the roots of quadratic equations to any polynominal with real coefficients

⇒ If f(z) is a polynominal with real coefficients, and z₁ is a root of f(z) = 0, then z₁* is also a root of f(z) = 0

• Note: if z₁ is real, then z₁* = Z₁

⇒ You can use this property to find roots of cubic and quartic equations with real coefficients

⇒ An equation of the form az³ + bz² + cz + d = 0 is called a cubic equation and has three roots

⇒ For a cubic equation with real coefficients, either:

• All three roots are real, or
• One root is real and the other two form a complex conjugate pair

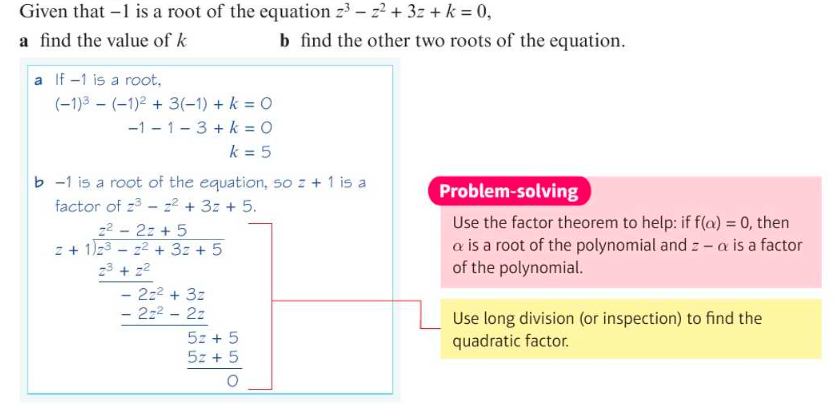
⇒ An equation of the form az⁴ + bz³ + cz² + dz + e = 0 is called a quartic equation and has four roots

⇒ For a cubic equation with real coefficients, either:

• All four roots are real, or
• Two roots are real and the other two form a complex conjugate pair, or
• Two roots form a complex conjugate pair and the other two form a complex conjugate pair

⇒ Watch out: a real valued quartic equation might have repeated roots or repeated complex roots

⇒ Also see our notes on:

• Imaginary and Complex Numbers
• Multiplying Complex Numbers
• Complex Conjugation
• Roots of Quadratic Equations